Vniřní statické účinky - Šwedlerovy věty (☕☕)

Metoda řezu je snadná, ale v případě obecného zatížení, které je popsané nějakou funkcí \(q(x)\), se stane rychle komplikovanou (výpočet těžiště uřízlé oblasti a obsah).

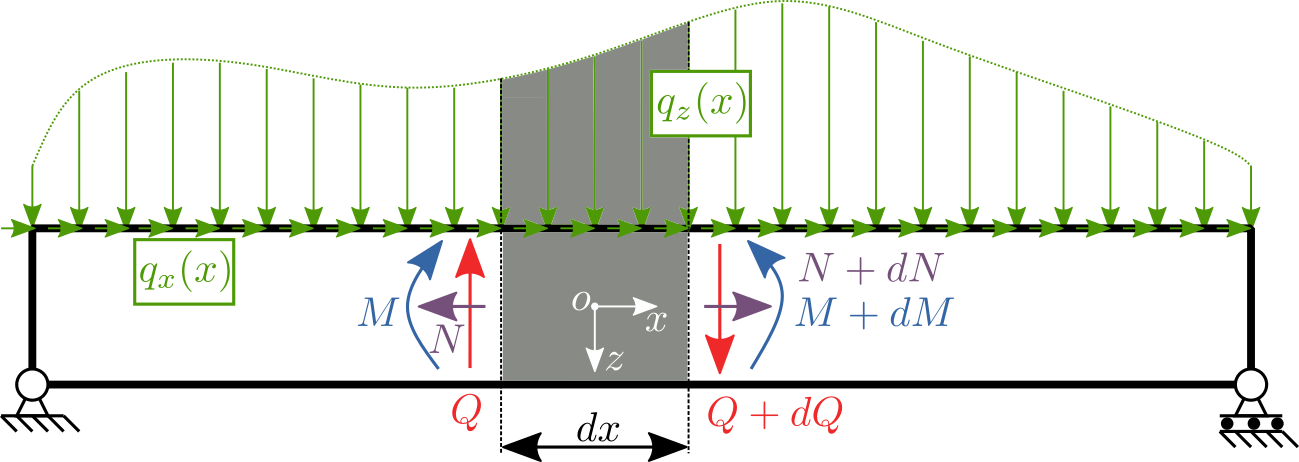
podle počtu stupňů volnosit zavedeme posouvající sílu \(N\), která je popisuje podélnou sílu v tělese. Dále zavedeme tečnou sílu \(Q\), která popisuje střižnou sílu a nakonec ohybový moment \(M\). Kladný směr volíme libovolně(opět platí, že musíme dodržovat po celý výpočet), ale doporučeno je zavádět orientaci podle obrázku. Pro známé spojité zatížení \(q_x(x)\) nebo \(q_z(x)\) vyřízněme nekonečně malý úsek a zaveďmě VSU podle zvyku. Silové rovnice rovnováhy pro \(N\) a \(Q\) vedou na diferenciální rovnici prvního řádu

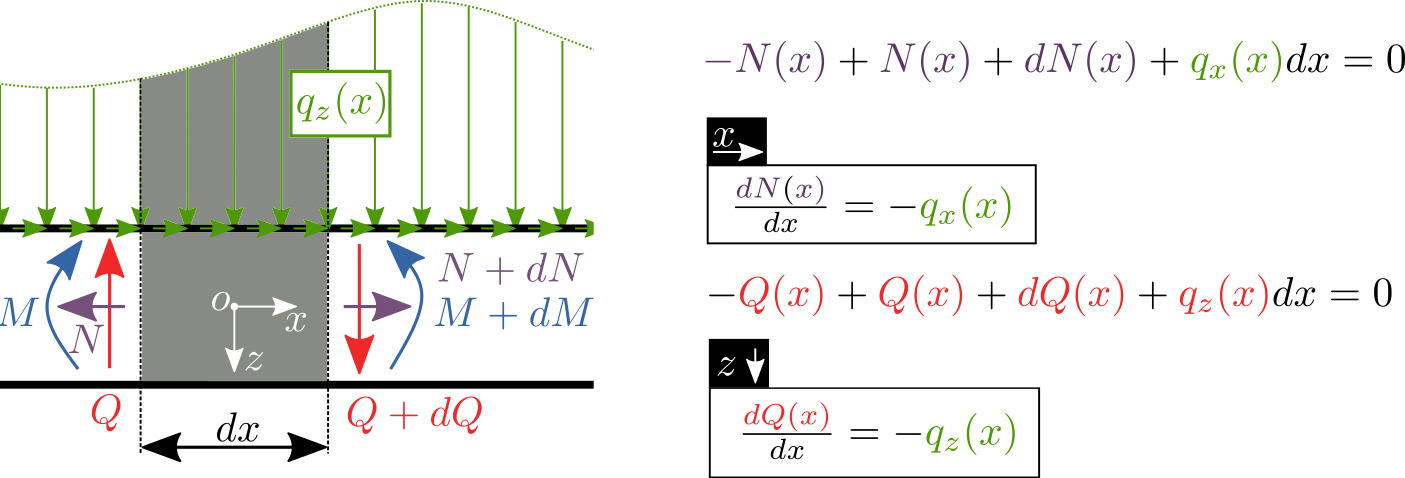
Podobnou úvahu aplikujme pro výpočet momentové rovnice rovnováhy. Z obrázku je patrné, že násobení dvou malých členů (\(dQdx\)) budeme uvažovat za velmi malý přírustek a tak ho zanedbáme. Z momentové rovnice opět získáme diferenciální rovnici pro moment.

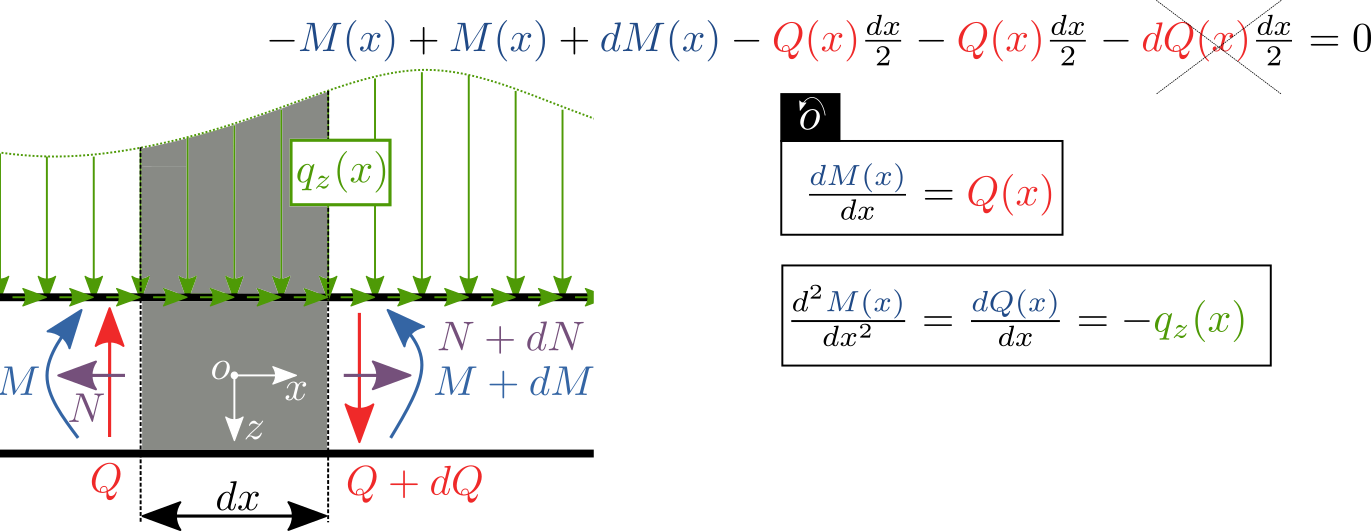
Je zřejmé, že mezi zatížením, silami a momentem existují vztahy, které popisují Šwedlerovy věty. Nalezené diferenciální rovnice lze řešit prostou separací proměnných a integrací, viz. následující příklad.

Příklad

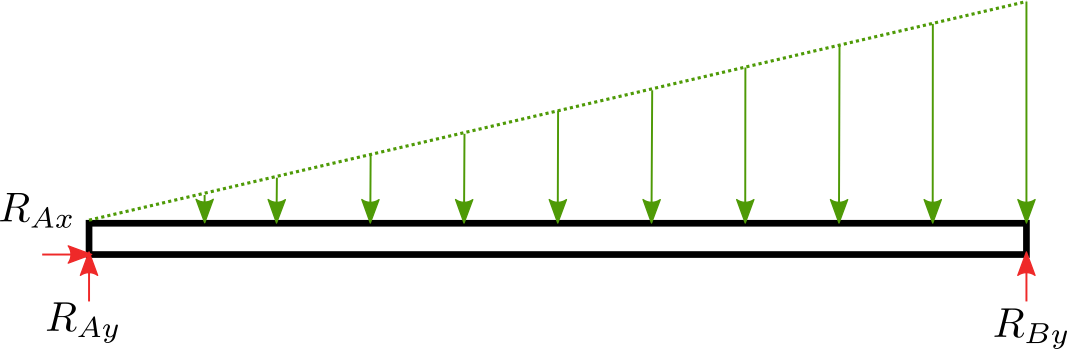
Nalezněte průběh posouvající síly \(N\), tečné síly \(Q\) a ohybového momentu \(M\) pro nosník uložený a zatížený podle obrázku:

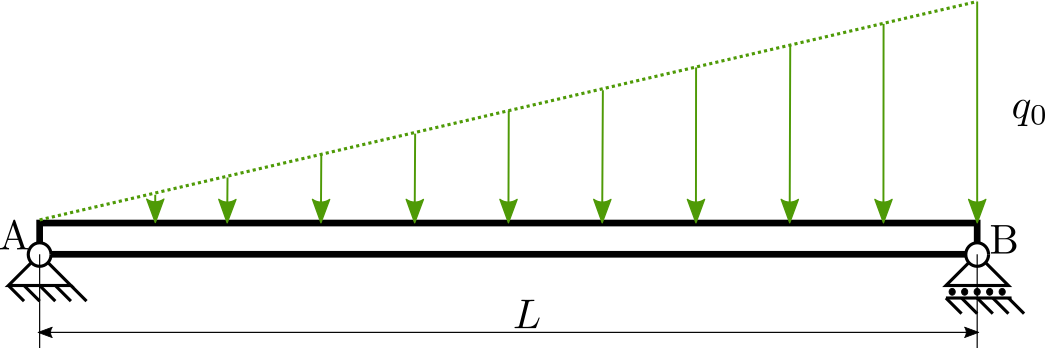
Konstanta zatížení \(q_0\)=5 N/m a vzdálenost podpor \(L\)=1 m.

Řešení

Nejdříve nosník uvolníme a napíšeme rovnice rovnováhy:

\[\begin{split} \begin{align} \overrightarrow{x}:& R_{Ax} =0 \\ y\uparrow:& R_{Ay} + R_{By} - \frac{Lq_0}{2}=0 \\ \overset{\curvearrowleft}{+M}: & R_{By}L - \frac{Lq_0}{2}\frac{2}{3}L=0 \end{align} \end{split}\]

import sympy as sp
q0, L = sp.symbols('q0 L')
RAx, RAy, RBy = sp.symbols('RAx RAy RBy')

eq1 = sp.Eq(RAx, 0)
eq2 = sp.Eq(RAy + RBy - L * q0 / 2, 0)
eq3 = sp.Eq(RBy * L - L * q0 / 2 * 2 / 3 * L, 0)

reseni = sp.solve([eq1, eq2, eq3], [RAx, RAy, RBy])
RAx = reseni[RAx]
RAy = reseni[RAy]
RBy = reseni[RBy]

sp.pprint(RAx)
sp.pprint(RAy)
sp.pprint(RBy)

0
L⋅q₀
────
 6  
L⋅q₀
────
 3  

Aplikace Šwedlerovy věty

nejdříve definujeme funkční předpis pro zatížení:

\[ \begin{equation} q(x) = \frac{q_0}{L}x \end{equation} \]

x = sp.symbols('x')
Q = sp.symbols('Q', cls=sp.Function) # jako funkce
q = q0 / L * x

vztah zatížení \(q(x)\) a tečné síly \(Q(x)\) (diff. rovnice):

\[ \begin{equation} \frac{dQ(x)}{dx} = - q(x) \end{equation} \]

Řešením je:

\[ \begin{equation} \int dQ(x) = -\int q(x)dx \end{equation} \]

drQ = sp.Eq(Q(x).diff(x), -q) # differencialni rovnice

res = sp.dsolve(drQ) # reseni differencialni rovnice
sp.pprint(res)

                2
            q₀⋅x 
Q(x) = C₁ - ─────
             2⋅L 

konstantu \(C_1\) neznáme, ale umíme jí spočítat ze znalostí reakcí \(R\):

\[ \begin{equation} Q(x=0) = R_{Ay} = C_1 \xrightarrow{} C_1= \frac{L q_0}{6} \end{equation} \]

po dosazení \(C_1\), vidíme, že tečná síla \(Q(x)\) má předpis:

\[ \begin{equation} Q(x) = \frac{Lq_0}{6} - \frac{q_0}{2L}x^{2} \end{equation} \]

import numpy as np
L = 1.
q0 = 5.
x = np.linspace(0, L, 10)

Qnum = L * q0 / 6. - q0 * x ** 2 / (2 * L)

Nalezení momentu \(M\)

vztah tečné síly \(Q(x)\) a momentu \(M(x)\) (diff. rovnice):

\[ \begin{equation} \frac{dM(x)}{dx} = Q(x) \end{equation} \]

M = sp.symbols('M', cls=sp.Function) # jako funkce
L, q0, x = sp.symbols('L q0 x') # sme si je prepsali na numeriku
Q = L * q0 / 6. - q0 * x ** 2 / (2 * L)

Řešením je:

\[ \begin{equation} \int dM(x) = \int Q(x)dx = \int\Big(\frac{Lq_0}{6} - \frac{q_0}{2L}x^{2}\Big)dx \end{equation} \]

drM = sp.Eq(M(x).diff(x), Q) # differencialni rovnice

res = sp.dsolve(drM) # reseni differencialni rovnice
sp.pprint(res)

                                                             3
                                       0.166666666666667⋅q₀⋅x 
M(x) = C₁ + 0.166666666666667⋅L⋅q₀⋅x - ───────────────────────
                                                  L           

konstantu \(C_1\) neznáme, ale umíme jí spočítat ze znalostí reakcí \(M\):

\[ \begin{equation} M(x=0) = 0 = C_1 \xrightarrow{} C_1= 0 \end{equation} \]

L = 1.
q0 = 5.
x = np.linspace(0, L, 10)
Mnum = q0 * x * (L ** 2 - x ** 2) / (6 * L)

import matplotlib.pylab as plt
plt.xkcd()
#nastavime velikost obrazku
fig, ax0 = plt.subplots(figsize=(15, 5))
q = q0 / L * x
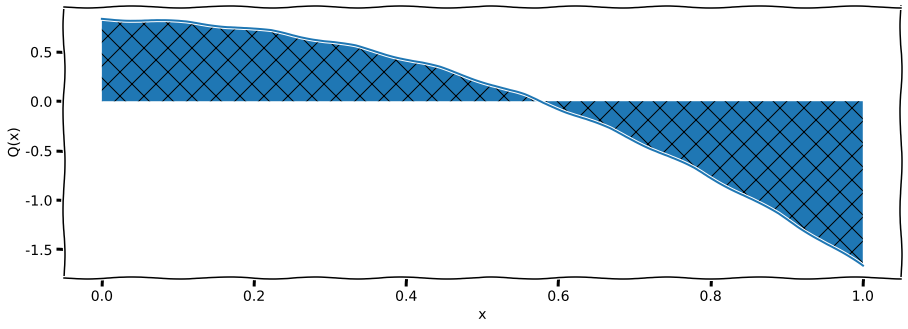
ax0.fill_between(x, Qnum, hatch="X", label="Q(x)");
ax0.plot(x, Qnum)
ax0.set_xlabel('x')
ax0.set_ylabel('Q(x)')
#nastavime velikost obrazku
fig, ax1 = plt.subplots(figsize=(15, 5))

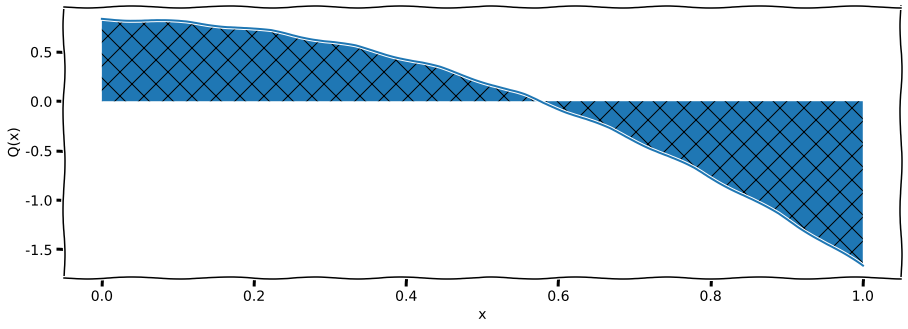
ax1.fill_between(x, Qnum, hatch="X", label="Q(x)");
ax1.plot(x, Qnum)
ax1.set_xlabel('x')
ax1.set_ylabel('Q(x)')

fig, ax2 = plt.subplots(figsize=(15, 5))
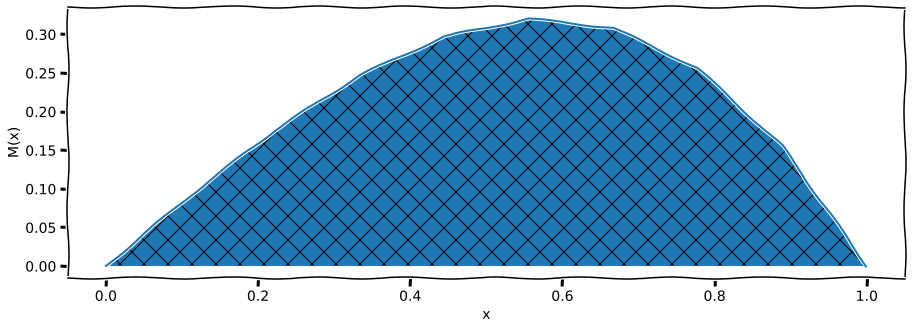
ax2.fill_between(x, Mnum, hatch="X", label="M(x)");
ax2.plot(x, Mnum) # podle definice swed. vety, + znamenko y dolu
ax2.set_xlabel('x')
ax2.set_ylabel('M(x)')

Text(0, 0.5, 'M(x)')

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Neue', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

Q

\[\displaystyle 0.166666666666667 L q_{0} - \frac{q_{0} x^{2}}{2 L}\]