Vnitřní statické účinky - metoda řezu (☕☕)#

Vnitřní statické účinky (VSU) jsou silové účinky v tělese. Budeme je studovat tak, že provedeme řez tělesem a vmístě řezu zavedeme odpovídající VSU podle obrázku.

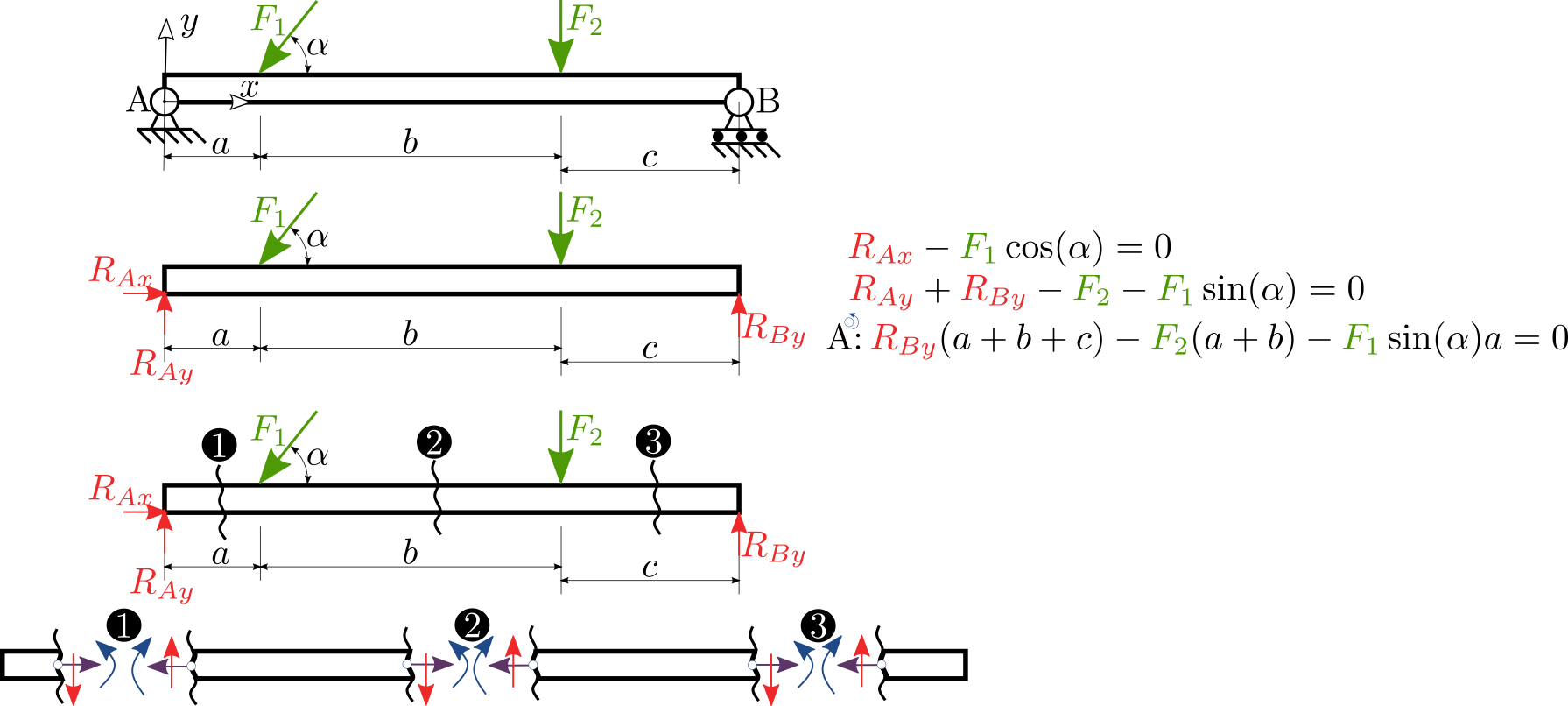
podle počtu stupňů volnosit zavedeme posouvající sílu \(N\), která je popisuje podélnou sílu v tělese. Dále zavedeme tečnou sílu \(Q\), která popisuje střižnou sílu a nakonec ohybový moment \(M\). Kladný směr volíme libovolně(opět platí, že musíme dodržovat po celý výpočet), ale doporučeno je zavádět orinetaci podle obrázku.

Postup#

Nejdříve analyzujeme zatížení nosníku a napíšeme vnější rovnice rovnováhy uvolněním nosníku a nahrazením uložení odpovídajícími reakcemi.
Řezy se provádějí v místech kde dochází ke změně, tj. působiště osamocené síly, uložení nebo spojitého zatížení (začátek, či konec), viz obrázek se třemi řezy.
Ke každému řezu napíšeme rovnice rovnováhy a určíme platnost řezu.

Příklad#

Analyzujte průběh tahových/tlakových a střihových sil a ohybového momentu tenkého nosníku prostě podepřeného a zatíženého osamělými silami. Síla \(F_1=500\) N je pod sklonem \(\alpha=45°\), síla \(F_2=250\) N. Vzdálenosti jsou: \(a=0.2\) m, \(b=0.65\) m a \(c=0.4\) m.

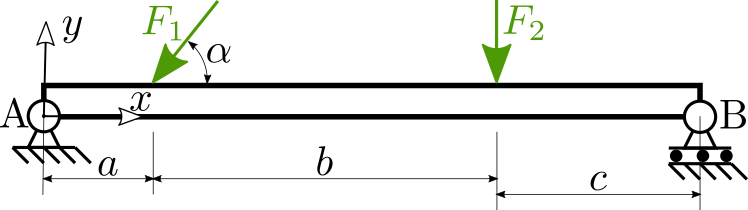
Určete:

a) Průběhy \(N\), \(Q\) a \(M\) podél nosníku
b) Maximální a minimální hodnoty VSÚ

Řešení#

Nejprve uvolníme nosník, zavedeme reakce a určíme PSV.

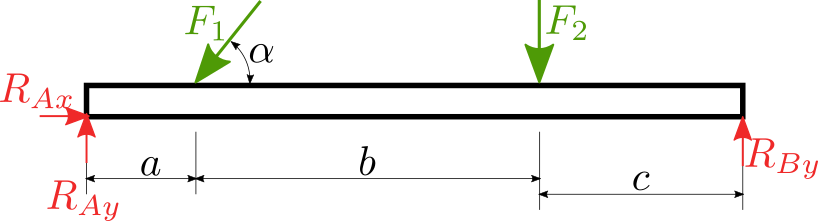
PSV = 0, protože máme 3 reakce a 3 rovnice rovnováhy (ve 2D), které jsou:

\[\begin{split} \begin{align} \overrightarrow{x}:& R_{Ax} - F_1\cos(\alpha)=0 \\ y\uparrow:& R_{Ay} + R_{By} - F_2 - F_1\sin(\alpha)=0 \\ \overset{\curvearrowleft}{+M}: & R_{By}(a+b+c)-F_2(a+b) - F_1\sin(\alpha)a=0 \end{align} \end{split}\]

import sympy as sp
F1, F2, a, b, c, alpha = sp.symbols('F1 F2 a b c alpha')
RAx, RAy, RBy = sp.symbols('RAx RAy RBy')

eq1 = sp.Eq(RAx - F1*sp.cos(alpha), 0)
eq2 = sp.Eq(RAy + RBy - F2 - F1 * sp.sin(alpha), 0)
eq3 = sp.Eq(RBy * (a + b + c) - F2 * (a + b) - F1*sp.sin(alpha)*a, 0)

reseni = sp.solve([eq1, eq2, eq3], [RAx, RAy, RBy])
RAx = reseni[RAx]
RAy = reseni[RAy]
RBy = reseni[RBy]

RAx

\[\displaystyle F_{1} \cos{\left(\alpha \right)}\]

RAy

\[\displaystyle \frac{F_{1} b \sin{\left(\alpha \right)} + F_{1} c \sin{\left(\alpha \right)} + F_{2} c}{a + b + c}\]

RBy

\[\displaystyle \frac{F_{1} a \sin{\left(\alpha \right)} + F_{2} a + F_{2} b}{a + b + c}\]

Řez č.1: \(x\in <0, a>\)#

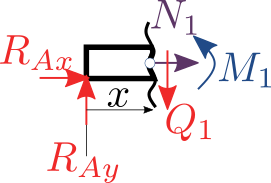
\[\begin{split} \begin{align} \overrightarrow{x}:& N_1 + R_{Ax}=0 \\ y\uparrow:& -Q_1 + R_{Ay}=0 \\ \overset{\curvearrowleft}{+M}: & M_1 - xR_{Ay}=0 \end{align} \end{split}\]

N1, Q1, M1, x = sp.symbols('N1 Q1 M1 x')
eq4 = sp.Eq(N1 + RAx, 0)
eq5 = sp.Eq(-Q1 + RAy, 0)
eq6 = sp.Eq(M1 - x * RAy,0)

reseni = sp.solve([eq4, eq5, eq6], [N1, Q1, M1])
N1 = reseni[N1]
Q1 = reseni[Q1]
M1 = reseni[M1]

N1

\[\displaystyle - F_{1} \cos{\left(\alpha \right)}\]

Q1

\[\displaystyle \frac{F_{1} b \sin{\left(\alpha \right)} + F_{1} c \sin{\left(\alpha \right)} + F_{2} c}{a + b + c}\]

M1

\[\displaystyle \frac{F_{1} b x \sin{\left(\alpha \right)} + F_{1} c x \sin{\left(\alpha \right)} + F_{2} c x}{a + b + c}\]

Řez č.2: \(x\in <a, a+b>\)#

\[\begin{split} \begin{align} \overrightarrow{x}:& N_2 + R_{Ax}-F_1\cos(\alpha)=0 \\ y\uparrow:& R_{Ay}-Q_2-F_1\sin(\alpha)=0 \\ \overset{\curvearrowleft}{+M}: & M_2 - x R_{Ay} + (x-a)F_1 \sin(\alpha)=0 \end{align} \end{split}\]

N2, Q2, M2 = sp.symbols('N2 Q2 M2')
eq7 = sp.Eq(N2 + RAx - F1 * sp.cos(alpha), 0)
eq8 = sp.Eq(RAy - Q2 -F1 * sp.sin(alpha), 0)
eq9 = sp.Eq(M2 - x * RAy + (x - a) * F1 * sp.sin(alpha),0)

reseni = sp.solve([eq7, eq8, eq9], [N2, Q2, M2])
N2 = reseni[N2]
Q2 = reseni[Q2]
M2 = reseni[M2]

N2

\[\displaystyle 0\]

Q2

\[\displaystyle \frac{- F_{1} a \sin{\left(\alpha \right)} + F_{2} c}{a + b + c}\]

M2

\[\displaystyle \frac{F_{1} a^{2} \sin{\left(\alpha \right)} + F_{1} a b \sin{\left(\alpha \right)} + F_{1} a c \sin{\left(\alpha \right)} - F_{1} a x \sin{\left(\alpha \right)} + F_{2} c x}{a + b + c}\]

Řez č.3: \(x\in <a+b, a+b+c>\)#

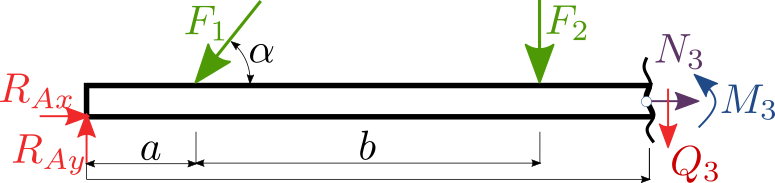
\[\begin{split} \begin{align} \overrightarrow{x}:& N_3 + R_{Ax}-F_1\cos(\alpha)=0 \\ y\uparrow:& R_{Ay}-Q_3-F_1\sin(\alpha) - F_2=0 \\ \overset{\curvearrowleft}{+M}: & M_3 - x R_{Ay} + (x-a)F_1 \sin(\alpha) + (x-a-b)F_2=0 \end{align} \end{split}\]

N3, Q3, M3 = sp.symbols('N3 Q3 M3')
eq10 = sp.Eq(N3 + RAx - F1 * sp.cos(alpha), 0)
eq11 = sp.Eq(RAy - Q3 - F1 * sp.sin(alpha) - F2, 0)
eq12 = sp.Eq(M3 - x * RAy + (x - a) * F1 * sp.sin(alpha) + (x-a-b) * F2,0)

reseni = sp.solve([eq10, eq11, eq12], [N3, Q3, M3])
N3 = reseni[N3]
Q3 = reseni[Q3]
M3 = reseni[M3]

N3

\[\displaystyle 0\]

Q3

\[\displaystyle \frac{- F_{1} a \sin{\left(\alpha \right)} - F_{2} a - F_{2} b}{a + b + c}\]

M3

Analýza výsledků#

# nahrajeme knihovnu na kresleni grafu a nastavime ji
import matplotlib.pylab as plt
plt.xkcd()
# nahrajeme numerickou knihovnu
import numpy as np
F1num = 500.
F2num = 250.
alphanum = sp.rad(45.)
anum, bnum, cnum = 0.2, 0.65, 0.4

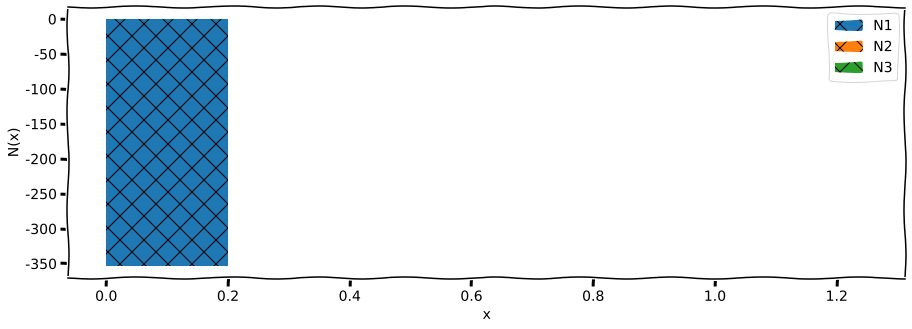
Průběh posouvající síly \(N\)#

# prevedeme symboliku na numeriku
N1num = sp.lambdify(x, N1.subs({F1:F1num, alpha:alphanum}))
N2num = sp.lambdify(x, N2)
N3num = sp.lambdify(x, N3)
# vytvorime vektor souradnice x pro kresleni
x1 = np.linspace(1e-16, anum, 100)
x2 = np.linspace(anum, anum + bnum, 100)
x3 = np.linspace(anum+bnum, anum+bnum+cnum, 100)

#nastavime velikost obrazku
plt.figure(figsize=(15, 5))
# kreslime
plt.fill_between(x1, N1num(x1) * x1/x1, label="N1", hatch="X")
plt.fill_between(x2, N2num(x2) * x2/x2, label="N2", hatch="X")
plt.fill_between(x3, N3num(x3) * x3/x3, label="N3", hatch="X")
#pojmenujeme osy
plt.xlabel("x")
plt.ylabel("N(x)")
#vykreslime legendu
plt.legend()
# posleme obrazek ven
plt.show()

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Neue', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

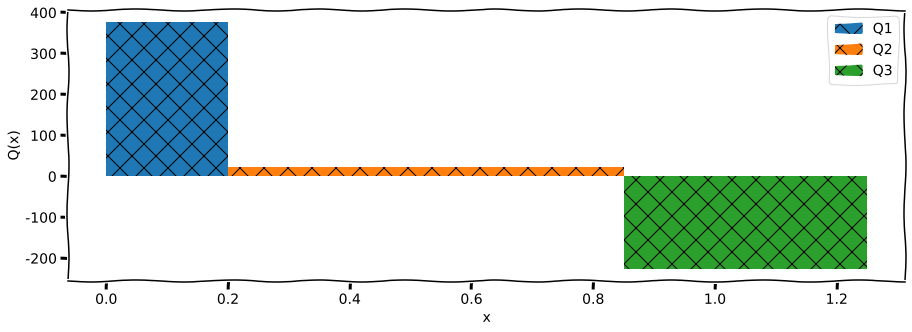
Průběh tečné síly \(Q\)#

Q1num = sp.lambdify(x, Q1.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
Q2num = sp.lambdify(x, Q2.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
Q3num = sp.lambdify(x, Q3.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
x1 = np.linspace(1e-16, anum, 100)
x2 = np.linspace(anum, anum + bnum, 100)
x3 = np.linspace(anum+bnum, anum+bnum+cnum, 100)

plt.figure(figsize=(15, 5))
plt.fill_between(x1, Q1num(x1), label="Q1", hatch="X")
plt.fill_between(x2, Q2num(x2), label="Q2", hatch="X")
plt.fill_between(x3, Q3num(x3), label="Q3", hatch="X")
plt.xlabel("x")
plt.ylabel("Q(x)")
plt.legend()
plt.show()

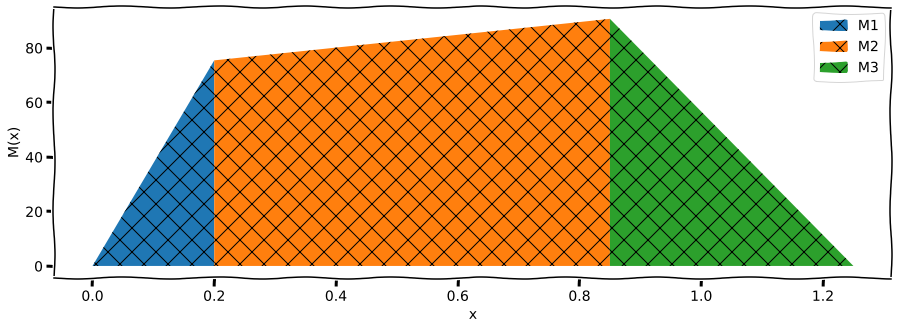
Průběh ohybového momentu \(M\)#

M1num = sp.lambdify(x, M1.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
M2num = sp.lambdify(x, M2.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
M3num = sp.lambdify(x, M3.subs({F1:F1num, alpha:alphanum, F2:F2num, a:anum, b:bnum, c:cnum}))
x1 = np.linspace(1e-16, anum, 100)
x2 = np.linspace(anum, anum + bnum, 100)
x3 = np.linspace(anum+bnum, anum+bnum+cnum, 100)

plt.figure(figsize=(15, 5))
plt.fill_between(x1, M1num(x1), label="M1", hatch="X")
plt.fill_between(x2, M2num(x2), label="M2", hatch="X")
plt.fill_between(x3, M3num(x3), label="M3", hatch="X")
plt.xlabel("x")
plt.ylabel("M(x)")
plt.legend()
plt.show()

Technické mechanika

Vnitřní statické účinky - metoda řezu (☕☕)

Contents