Účinky síly (☕)

Koncept síly

Síla je projevem interakce dvou těles nebo působení setrvačných a gravitačních účinků na těleso. Sílu rozdělíme na:

• statickou: nemění pohybový stav tělesa, tj. všechny síly jsou v rovnováze

• dynamicou: změna pohybového stavu tělese, vyjádřitelnou 2 Newtonovým zákonem:

\[ \overrightarrow{F} = \frac{d(m\overrightarrow{v})}{dt} \]

Zaveďme vhodný matematický popis. Uvažujme sílu jako vektor v kártézských souřadnicích:

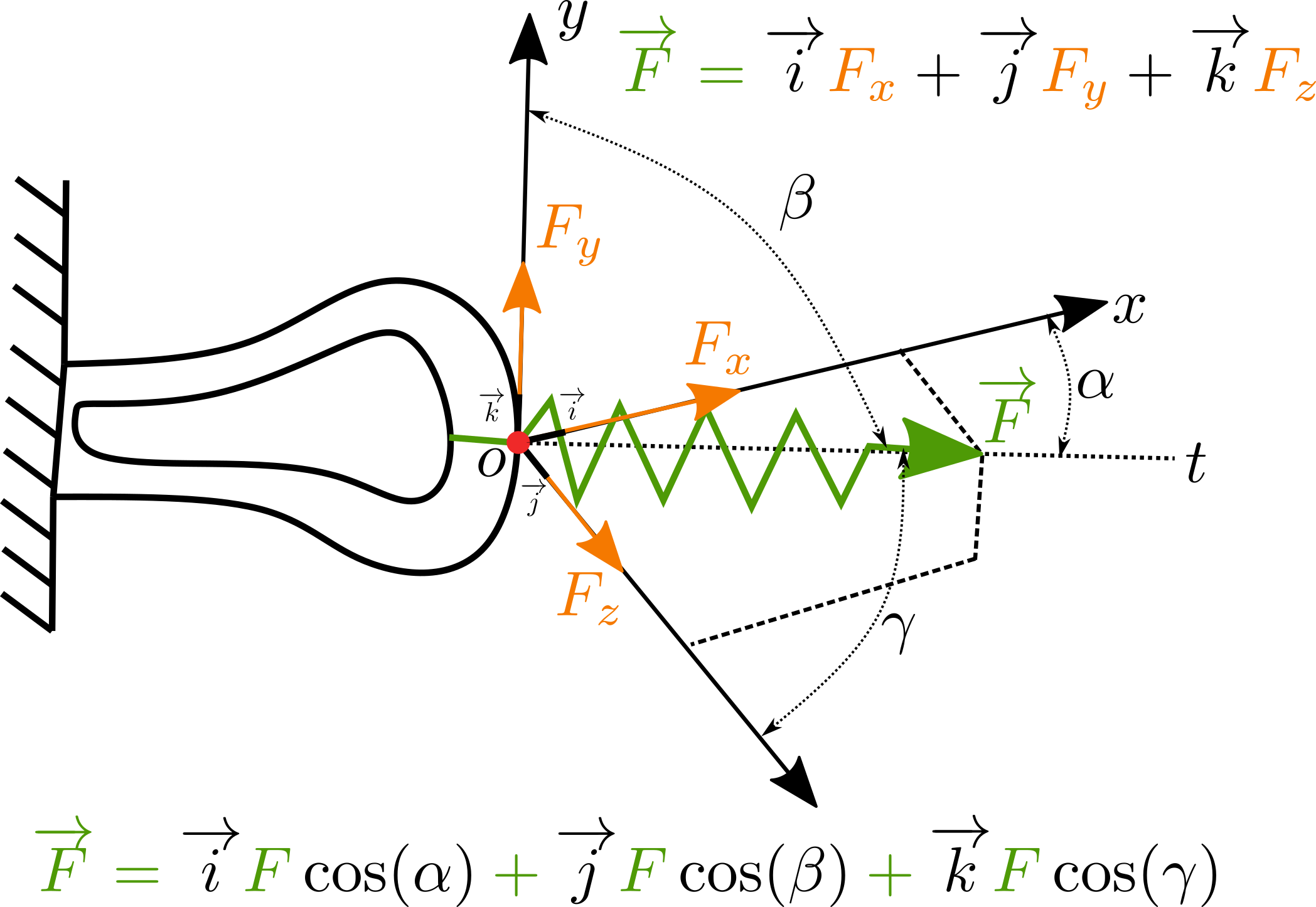
Sílu můžeme rozložit do směru souřadnic na složky (tohoto rozkladu budeme dále hojně využívat). Velikost vektoru pak lze snadno spočítat:

\[ F=\lVert\overrightarrow{F}\rVert=\sqrt{F_{x}^{2} + F_{y}^{2} + F_{z}^{2}} \]

Síla je orientovaný vektor, leží na přímce a prochází bodem (nebo působištěm).

Rozdělení silového působení

Silové působení můžeme rozdělit tři kategorie:

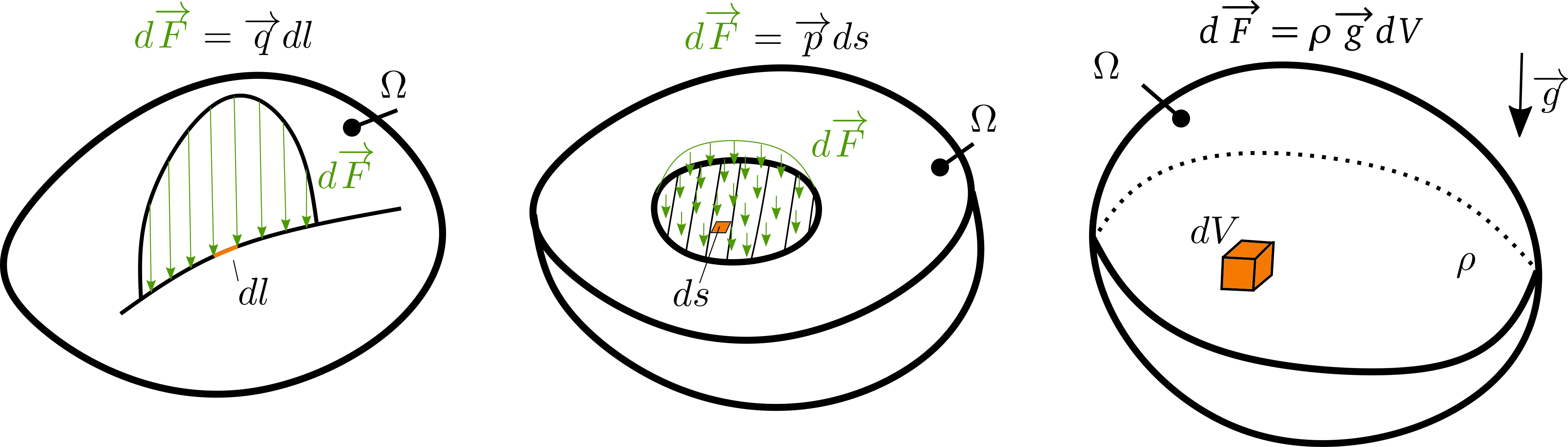
Liniové zatížení (obrázek vlevo) si lze představit jako zatížení přes hranu. Celková síla od liniového zatížení je pak dána jako integrál přes funkci zatížení \(\overrightarrow{q}\):

\[ \overrightarrow{F} = \int_{l}\overrightarrow{q}dl \]

Podobně platí i pro výpočet síly, která je dána plošnou intenzitou \(\overrightarrow{p}\):

\[ \overrightarrow{F} = \int_{S}\overrightarrow{p}ds \]

A nakonec objemové síly, dané například gravitací lze formulovat:

\[ \overrightarrow{F} = \int_{V}\rho\overrightarrow{g}dV \]

Otáčivé účinky síly

Definujme nejdříve sílu \(\overrightarrow{F}\) a její složky \(\{F_x, F_y, F_z\}\) a stejně tak rameno \(\overrightarrow{r}\) a jeho složky \(\{x_r, y_r, z_r\}\). Síla na \(\overrightarrow{F}\) na rameni \(\overrightarrow{r}\) způsobí otáčivý účinek k bodu \(o\) souřadnicového systému, \(\overrightarrow{M}_{o}\)

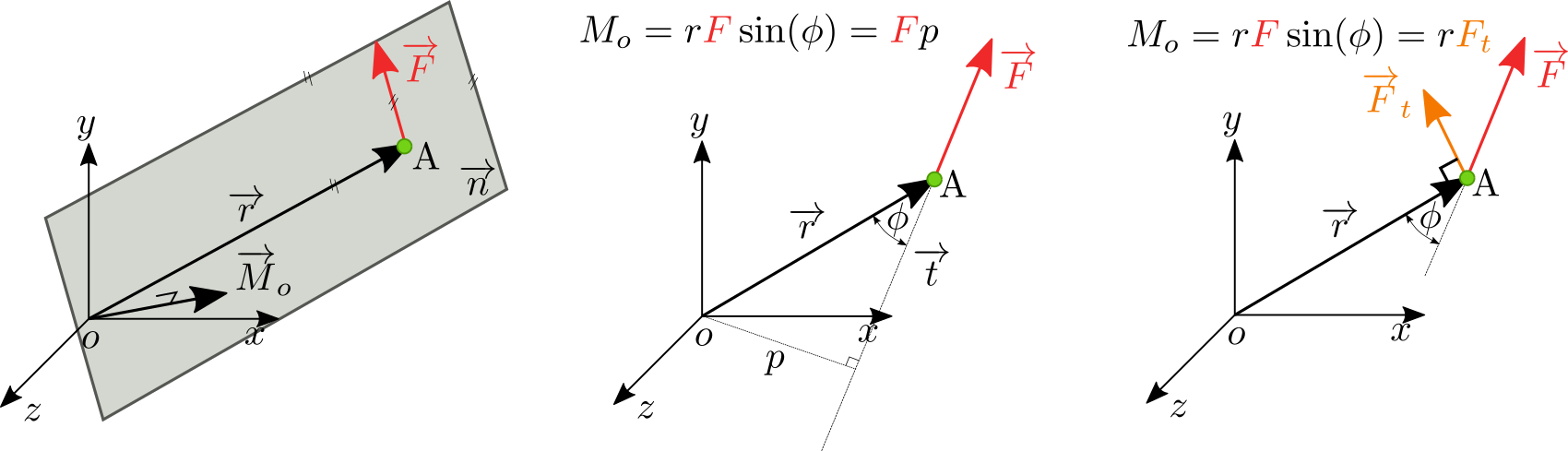
Moment \(\overrightarrow{M}_o\) je vektor, který je kolmý na \(\overrightarrow{r}\) a sílu \(\overrightarrow{F}\) a proto je dán vektorovým součinem

\[\begin{split} \begin{equation} \overrightarrow{M}_o = \begin{bmatrix} \overrightarrow{i} & \overrightarrow{j} & \overrightarrow{k} \\ x_r & y_r & z_r \\ F_x & F_y & F_z \end{bmatrix} = \overrightarrow{i}\begin{bmatrix} y_r & z_r \\ F_y & F_z \end{bmatrix} - \overrightarrow{j}\begin{bmatrix} x_r & z_r \\ F_x & F_z \end{bmatrix} + \overrightarrow{k}\begin{bmatrix} x_r & y_r \\ F_x & F_y \end{bmatrix} \end{equation} \end{split}\]

Nutno podotknout, že vektorový součin \(\times\) není komutativní a tedy záleží na pořádí násobení členů! Po rozepsání vektorového součinu vidíme

\[ \begin{equation} \overrightarrow{M}_o = \overrightarrow{i}(y_r F_z-z_r F_y) + \overrightarrow{j}(z_r F_x - x_r F_z)+\overrightarrow{k}(x_r F_y - y_r F_x) \end{equation} \]

Vhodným zpřeházením pořadí členů, lze získat zápis, který ukazuje, že moment \(\overrightarrow{M}_o\) lze zapsat jako součet dílčích momentů složek síly

\[ \begin{equation} \overrightarrow{M}_o = \overrightarrow{r}\times\left( \overrightarrow{F}_x+\overrightarrow{F}_y + \overrightarrow{F}_z \right) = \sum_{i=1}^{i=n}\overrightarrow{M}_{oi} \end{equation} \]

Otáčové účinky síly k ose

Dalším případem je stanovení otáčivého momentu \(\overrightarrow{M}_e\) k přímce, popsané směrovým vektorem \(\overrightarrow{e}\)

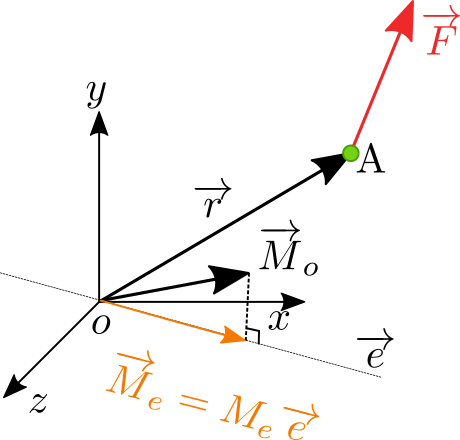
Moment k ose \(\overrightarrow{e}\) je vlastně projekcí \(\overrightarrow{M}_o\) do přímky \(\overrightarrow{e}\). Jinými slovy, tuto projekci snadno spočítáme pomocí skalárního součinu

\[ \begin{equation} \overrightarrow{M}_e=\underbrace{\left[\left(\overrightarrow{r}\times\overrightarrow{F}\right)\cdot\overrightarrow{e}\right]}_{M_e}\overrightarrow{e} \end{equation} \]

Moment silové dvojice

Uvažujme případ dvou sil \(\overrightarrow{F}_1 = \overrightarrow{F}\) a \(\overrightarrow{F}_2=-\overrightarrow{F}\). Podle obrázku platí

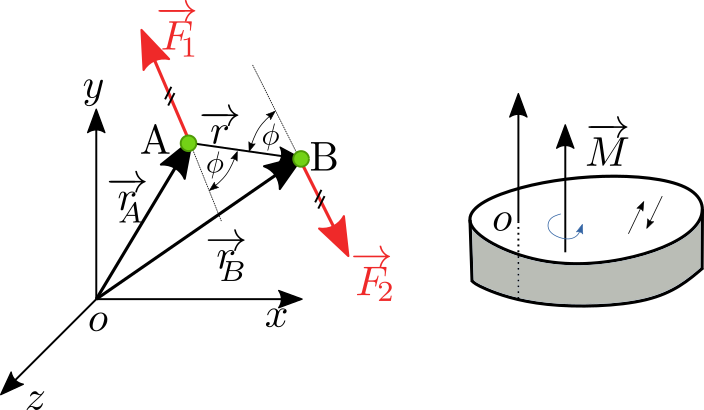
že vásledný moment \(\overrightarrow{M}_o\) k počátku \(o\) je

\[ \begin{equation} \overrightarrow{M}_o = \overrightarrow{r}_A \times \overrightarrow{F}_1 + \overrightarrow{r}_B \times \overrightarrow{F}_2=\overrightarrow{r}\times\overrightarrow{F} \end{equation} \]

Výsledný moment \(M_o\) je stejný po celém tělese, tedy je stejný k libovolnému bodu, protože

\[ \begin{equation} M_o=rF\sin(\phi)=konstanta!,\ (\overrightarrow{M}_o=\overrightarrow{M}_a) \end{equation} \]

Příklady k procvičení

Na tomto cvičení jsou představeny příklady na skládání sil a výpočet momentů. Komentované příklady od Petry Tisovské naleznete zde