Mechanizmy(☕☕☕)

Klasifikace

Mechanismy je možno rozdělit na rovinné a prostorové. U rovinných mechanismů (i když jsou prostorově konstruovány) všechny body mechanismu se pohybují v rovinách rovnoběžných, osy rotací jsou rovnoběžné, při grafickém znázorňování jsou tyto osy kolmé na roviny pohybů. Členy mechanismů nemusí být rovinné útvary tj. desky- např. klikový mechanismus spalovacího motoru. U prostorových mechanismů konají jednotlivá tělesa vzhledem k rámu nebo vůči sobě prostorové pohyby.

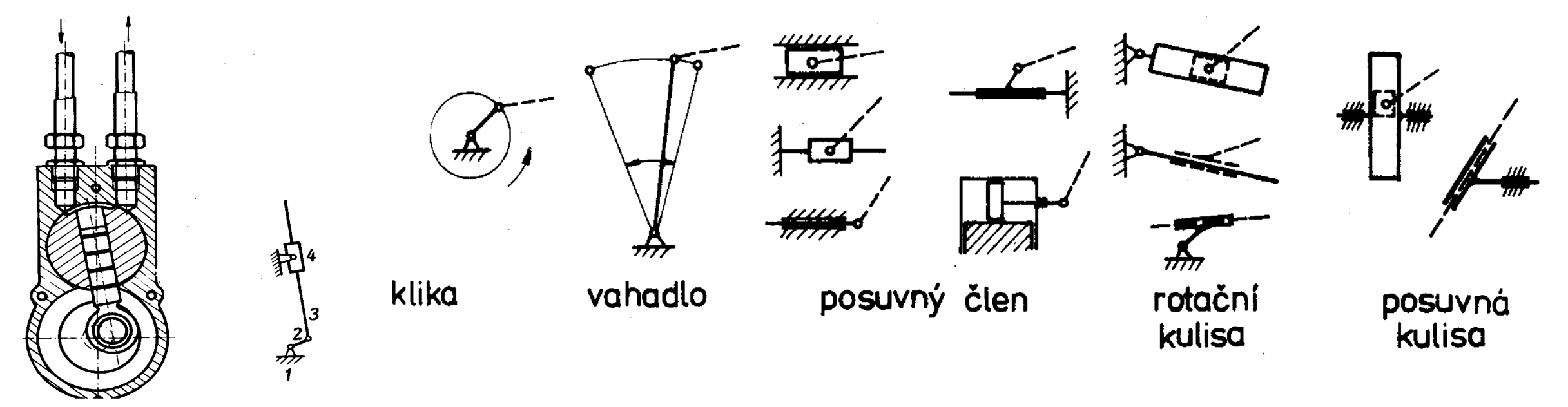
Nejčastěji se vyskytují mechanismy, které mají jeden stupeň volnosti. Má-li mechanismus dva stupně volnosti, nazývá se diferenciál.

Převodová funkce

Podle převodu se mechanismy dělí na mechanismy s konstantním převodem (závislost hnané souřadnice na hnací je lineární) a mechanismy s nekonstantním převodem(závislost hnaných souřadnic na hnací je nelineární).Závislost souřadnice hnaného členu \(\Psi\) na hnací souřadnici \(\phi\) nazýváme zdvihovou závislostí:

\[ \begin{equation} \Psi = \lambda(\phi) \end{equation} \]

Itá derivace je pak itá převodová funkce:

\[ \begin{equation} \mu_{i} = \frac{d^i\Psi}{d\phi^i} \end{equation} \]

Vektorová smyčka: problém

Uvažujme těleso, které vykonává otáčivý a posuvný pohyb:

Zavěďme dva souřadnicové systémy (SS): globální a lokální a uvažujme těleso dokonale tuhé. Vektoy ve vektorové smyčce lze sčítat jen v rámci jednoho souřadnicového systému a tak musí být všechny vektory transformovány podle potřeby.

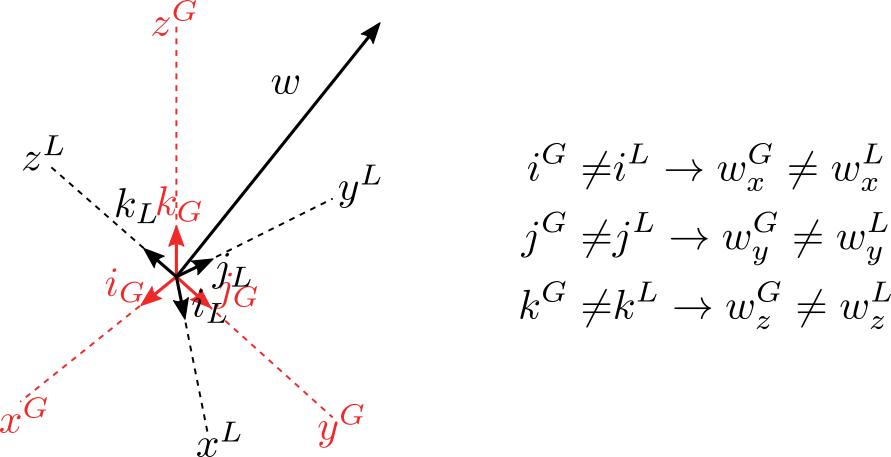
Oba SS prochází stejným počátkem pro jednoduchost. Uvažujme dva SS, které mají společný počátek a vyjádřeme kosíny os lokálního SS v globálním SS.

• \(\mathrm{T}\) je ortogonální (\(\mathrm{T}^{-1}=\mathrm{T}^T\))

• \(\mathrm{T}(\phi(t))\): \(r_B(t) = r_L(t) + \mathrm{T}^{GL}(t)r_{LB}\)

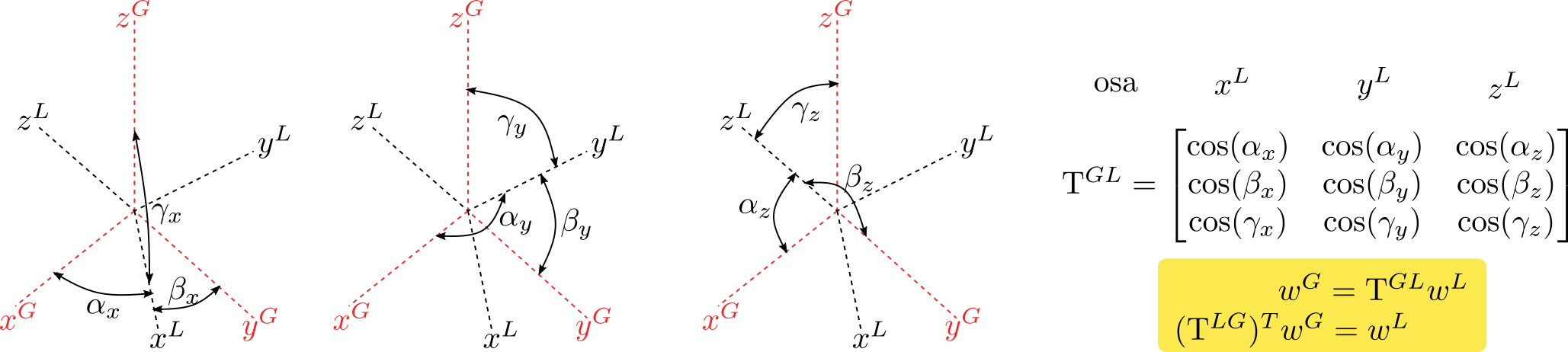
Transformační matice \(\mathrm{T}\) obsahuje 9 neznámých úhlů. Pro \(r_B\) dokonce 12 neznámých. Úhly nejsou nezávislé a splňují vazebné podmínky:

\[\begin{split} \begin{align} \cos(\alpha_x)^2+\cos(\beta_x)^2 + \cos(\gamma_x)^2 = & 1 \\ \cos(\alpha_y)^2+\cos(\beta_y)^2 + \cos(\gamma_y)^2 = & 1 \\ \cos(\alpha_y)^2+\cos(\beta_y)^2 + \cos(\gamma_y)^2 = & 1 \\ i_L\cdot j_L = & 0 \\ j_L\cdot k_L = & 0 \\ k_L\cdot i_L = & 0 \end{align} \end{split}\]

Tedy 6 rovnic odebere přebývajících 6 stupňů volnosti.

Speciální případ \(\mathrm{T}^{GL}\) pro 2D

Uvažujme globální a lokální SS, které mají společný počátek a platí, že \(z^G = z^L\)

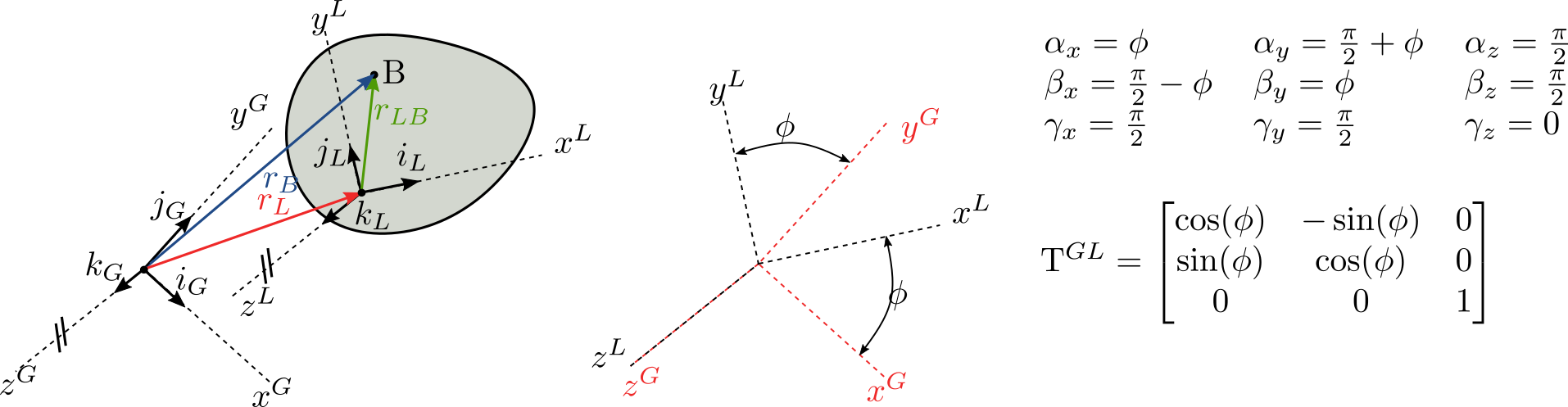
• \(\mathrm{T}(\phi(t))\): \(r_B^G(t) = r_L^G(t) + \mathrm{T}^{GL}(t)r_B^L\) (přejdeme k zápisu zohledňující SS.)

• rychlost: \(\dot{r}_B^G=\dot{r}_L^G + \dot{\mathrm{T}}^{GL}r_B^G + \mathrm{T}^{GL}\dot{r}_B^L\)

• zrychlení: \(\ddot{r}_B^G=\ddot{r}_L^G + \ddot{\mathrm{T}}^{GL}r_B^G + 2\dot{\mathrm{T}}^{GL}\dot{r}_B^G + \mathrm{T}^{GL}\ddot{r}_B^L\)

Některé členy budeme považovat za konstantní: \(r_B^L\), časová derivace transformační matice \(\mathrm{T}^{GL}\) je:

\[\begin{split} \begin{equation} \dot{\mathrm{T}}^{GL} = \begin{bmatrix} -\sin(\phi) & -\cos(\phi) & 0 \\ \cos(\phi) & -\sin(\phi) & 0 \\ 0 & 0 & 0 \end{bmatrix}\dot{\phi} \end{equation} \end{split}\]

a zrychlení:

\[\begin{split} \begin{equation} \ddot{\mathrm{T}}^{GL} = \begin{bmatrix} -\cos(\phi) & \sin(\phi) & 0 \\ -\sin(\phi) & -\cos(\phi) & 0 \\ 0 & 0 & 0 \end{bmatrix}\dot{\phi}^2 + \begin{bmatrix} -\sin(\phi) & -\cos(\phi) & 0 \\ \cos(\phi) & -\sin(\phi) & 0 \\ 0 & 0 & 0 \end{bmatrix} \ddot{\phi} \end{equation} \end{split}\]

poznámka: \(\dot{w}^L = (\mathrm{T}^{GL})^T\dot{\mathrm{T}}^{GL}w^G\)

Příklad 01: svázané body

Uvažujte dokonalé lano bez tření, které se odvíjí z bubnu o poloměru \(R\). Na konci lana je bod \(A\), který se pohybuje vodorovně konstantní rychlostí \(v_A\).

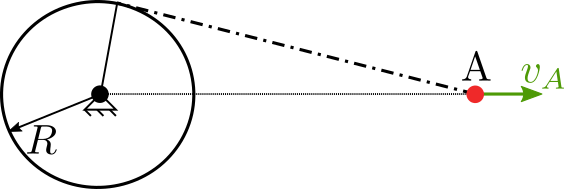
Určete:

• a) průběh natočení \(\phi\) na čase \(t\)

• b) průběh úhlové rychlosti \(\omega\) na čase \(t\)

• c) průběh úlového zrychlení \(\alpha\) na čase \(t\)

• d) obvodovou rychlost \(v_A'\) bubnu na čase \(t\)

Řešení

Nejdříve zavedeme sledované a pomocné veličiny:

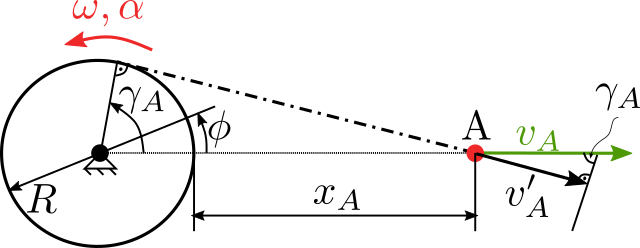
Je zřejmé, že:

\[ \begin{equation} v'_A = v_A\sin(\gamma_A) \end{equation} \]

také, že \(x_A = v_A t\) a \(\cos(\gamma_A) = \frac{R}{R+x_A}\)

Pomocný úhel \(\gamma_A\) lze snadno nahradit (gon.identita):

\[ \begin{equation} \Big(\frac{R}{R+x_A}\Big)^2 + \Big(\frac{v'_A}{v_A}\Big)^2 = 1 \tag{1} \end{equation} \]

Obvodou rychlost bubunu známe! Proto:

\[ \begin{equation} v'_A = \omega R \end{equation} \]

dosadíme do (1):

\[ \begin{equation} \omega = \pm \frac{v_A}{R}\sqrt{1-\Big(\frac{R}{R + x_A}\Big)^2} = - \frac{v_A}{R}\sqrt{1-\Big(\frac{1}{1 + \frac{v_A t}{R}}\Big)^2} \tag{2} \end{equation} \]

Zrychlení \(\alpha\) je dáno derivací \(\dot{\omega}\):

import sympy as sp
R, v_A, t = sp.symbols('R v_A t', real=True, positive=True)
omega = -v_A / R * sp.sqrt(1 - (1 / (1 + (v_A * t / R)))**2)
alpha = sp.diff(omega, t)
alpha

\[\displaystyle - \frac{v_{A}^{2}}{R^{2} \left(1 + \frac{t v_{A}}{R}\right)^{3} \sqrt{1 - \frac{1}{\left(1 + \frac{t v_{A}}{R}\right)^{2}}}}\]

Výpočet natočení \(\phi\) vychází z diff. rovnice \(\omega = \dot{\phi}\):

\[ \begin{equation} \int_{0}^{\phi} d\phi = -\int_0^t \frac{v_A}{R}\sqrt{1-\Big(\frac{1}{1 + \frac{v_A t}{R}}\Big)^2} dt \end{equation} \]

Pro řešení intregrálu zaveďme substituci: \(u = 1 + \frac{v_At}{R}\), differenciál je pak \(du=\frac{v_A}{R}dt\), integrál přepíšeme:

\[ \begin{equation} \int_0^{\phi} d\phi = -\int_1^{1+\frac{v_At}{R}}\sqrt{1 - \frac{1}{u^2}} du \end{equation} \]

phi = sp.symbols('phi', cls=sp.Function)
u = sp.symbols('u', real=True, positive=True)
dr_phi = sp.Eq(phi(u).diff(u), - sp.sqrt(u**2 - 1)/u) # differencialni rovnice
res = sp.dsolve(dr_phi, phi(u)) # reseni differencialni rovnice
res

\[\begin{split}\displaystyle \phi{\left(u \right)} = C_{1} - \begin{cases} - \frac{i u^{2}}{\sqrt{1 - u^{2}}} - i \operatorname{acosh}{\left(\frac{1}{u} \right)} + \frac{i}{\sqrt{1 - u^{2}}} & \text{for}\: \frac{1}{u^{2}} > 1 \\\frac{u^{2}}{\sqrt{u^{2} - 1}} + \operatorname{asin}{\left(\frac{1}{u} \right)} - \frac{1}{\sqrt{u^{2} - 1}} & \text{otherwise} \end{cases}\end{split}\]

Řešení diff. rovnice je komplikované, tak přejdeme k numerice:

from scipy.integrate import odeint
import numpy as np

def omega_fun(phi, t, v_A, R):
    return -v_A / R * np.sqrt(1 - (1. / (1. + (v_A * t / R))) ** 2)

v_A_num, R_num = 1, 1
phi_0 = 0.
tn = np.linspace(0, 3, 101)
phin = odeint(omega_fun, phi_0, tn, args=(v_A_num, R_num))

import matplotlib.pyplot as plt

omegan = sp.lambdify(t, omega.subs({v_A:v_A_num, R:R_num}))
alphan = sp.lambdify(t, alpha.subs({v_A:v_A_num, R:R_num}))

plt.xkcd()
plt.figure(figsize=(15, 5))
plt.plot(tn, phin, label=r'$\phi$')
plt.plot(tn, omegan(tn), label=r'$\omega$')
plt.plot(tn, alphan(tn), label=r'$\alpha$')
plt.legend()
plt.xlabel(r'cas [t]')
plt.show()

<lambdifygenerated-2>:2: RuntimeWarning: divide by zero encountered in true_divide
  return -1/(sqrt(1 - 1/(t + 1)**2)*(t + 1)**3)
findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Neue', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Neue', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

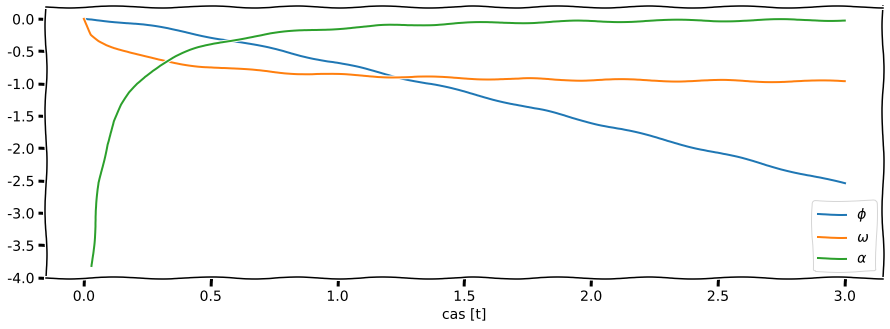
Příklad 02: Zdvihací rameno

Uvažujte jednoduché robotické rameno podle obrázku.

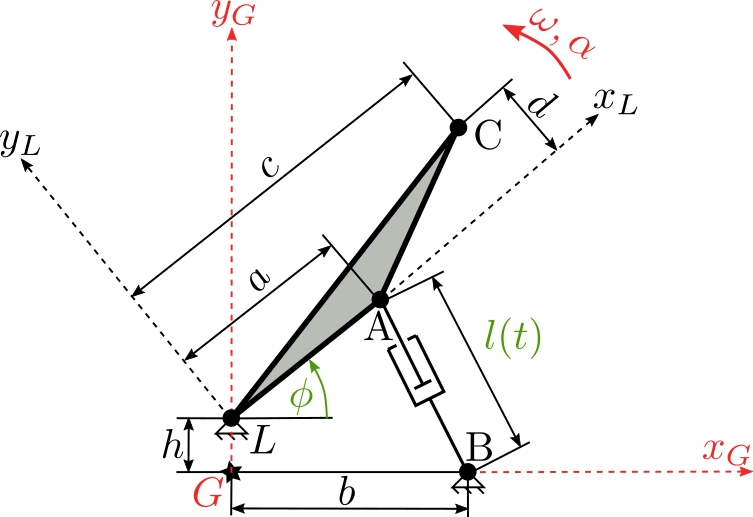
Pro zadané parametry \(a, b, c, d, L, T\) a lineární servo pohon jehož předpis pro polohu je \(l(t)=4L\frac{t}{T}(1 - \frac{t}{T})\)

určete:

• a) průběh natočení \(\phi\) na čase \(t\)

• b) průběh úhlové rychlosti \(\omega\) na čase \(t\)

• c) průběh úlového zrychlení \(\alpha\) na čase \(t\)

• d) zdvihovou funkci \(\Psi\)

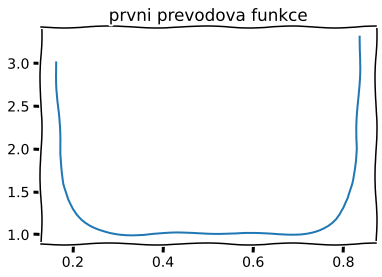
• e) 1. převodou funkci \(\mu\)

Řešení

Nejdříve formulujeme globální a lokální polohové vektory: \(r_L^G = \begin{bmatrix}0 \\ h \\ 0\end{bmatrix}\); \(r_B^G = \begin{bmatrix}b \\ 0 \\ 0\end{bmatrix}\); \(r_A^L = \begin{bmatrix}a \\ 0 \\ 0\end{bmatrix}\); \(r_C^L = \begin{bmatrix}c \\ d \\ 0\end{bmatrix}\)

Dále sestavíme vektorovu rovnici pro bod A v globálním SS:

\[ \begin{equation} r_A^G = r_L^G + \mathrm{T}^{GL}r_A^L \tag{1} \end{equation} \]

Výpočet natočení \(\phi\)

Abychom zohlednili proměnnou vzdálenost bodů A a B, předepsanou funkcí \(l(t)\), formulujeme vektor \(r_{AB}^G=r_A^G - r_B^G\). Snadno zjistíme, že:

\[ \begin{equation} r_{AB}^G\cdot r_{AB}^G = l^2(l) \tag{2} \end{equation} \]

A tedy platí, že rozšíření (1):

\[ \begin{equation} r_A^G - r_B^G = r_L^G -r_B^G + \mathrm{T}^{GL}r_A^L \tag{3} \end{equation} \]

import sympy as sp
L, T = sp.symbols('L T')
phi, a, b, c, d, h, t = sp.symbols('phi a b c d h t')
r_x = -b + a * sp.cos(phi)
r_y = h + a * sp.sin(phi)
l = 4 * L * t / T * (1. - t / T)

eq2 = sp.Eq(r_x ** 2 + r_y ** 2, l**2)
res = sp.solve(eq2, phi)
phi=res[0] # vyber reseni
phi

\[\displaystyle - 2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)}\]

Výpočet úhlové rychlosti \(\omega\)

Přepíšeme rovnici (4) na:

\[ \begin{equation} -b\cos(\phi) + h\sin(\phi) = \frac{l^2(t) - a^2 - b^2 - h^2}{2a} \end{equation} \]

a implicitně zderivujeme:

\[ \begin{equation} b\sin(\phi)\dot{\phi} + h\cos(\phi)\dot{\phi} = \frac{l}{a}\dot{l}(t \rightarrow \dot{\phi} = \frac{l(t)}{a(b\sin(\phi)+h\cos(\phi))}\dot{l}(t) \tag{5} \end{equation} \]

kde \(\dot{l}(t) = \frac{4L}{T}(1-2\frac{t}{T})\)

dldt = l.diff(t)
dldt.simplify()
dldt

\[\displaystyle \frac{4 L \left(1.0 - \frac{t}{T}\right)}{T} - \frac{4 L t}{T^{2}}\]

omega = l / a / (b * sp.sin(phi) + h * sp.cos(phi)) * dldt

Výpočet úhlového zrychlení \(\alpha\)

Opět implicitně zderivujeme výraz (5):

\[ \begin{equation} b\cos(\phi)\dot{\phi}^2 + b\sin(\phi)\ddot{\phi} - h\sin(\phi)\dot{\phi}^2 + h\cos(\phi)\ddot{\phi} = \frac{1}{a}\Big(\dot{l}^2(t) + l(t)\ddot{l}(t)\Big) \end{equation} \]

\[ \begin{equation} \rightarrow \alpha = \frac{\dot{l}^2(t) + l(t)\ddot{l}(t) - a\Big(b\cos(\phi) - h\sin(\phi)\Big)\dot{\phi}^2}{a\Big(b\sin(\phi) + h\cos(\phi)\Big)} \end{equation} \]

d2ldt2 = dldt.diff(t)
alpha = (dldt ** 2 + l * d2ldt2 - a * (b * sp.cos(phi) - h * sp.sin(phi)) * omega ** 2) \
         / a / (b * sp.sin(phi) + h * sp.cos(phi))

alpha

\[\displaystyle \frac{- \frac{16 L^{2} t^{2} \left(1.0 - \frac{t}{T}\right)^{2} \left(b \cos{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)} + h \sin{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)}\right) \left(\frac{4 L \left(1.0 - \frac{t}{T}\right)}{T} - \frac{4 L t}{T^{2}}\right)^{2}}{T^{2} a \left(- b \sin{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)} + h \cos{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)}\right)^{2}} - \frac{32 L^{2} t \left(1.0 - \frac{t}{T}\right)}{T^{3}} + \left(\frac{4 L \left(1.0 - \frac{t}{T}\right)}{T} - \frac{4 L t}{T^{2}}\right)^{2}}{a \left(- b \sin{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)} + h \cos{\left(2.0 \operatorname{atan}{\left(\frac{2.0 T^{4} a h - 39.1918358845308 \sqrt{- 0.166666666666667 L^{4} T^{4} t^{4} + 0.666666666666667 L^{4} T^{3} t^{5} - L^{4} T^{2} t^{6} + 0.666666666666667 L^{4} T t^{7} - 0.166666666666667 L^{4} t^{8} + 0.0208333333333333 L^{2} T^{6} a^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} b^{2} t^{2} + 0.0208333333333333 L^{2} T^{6} h^{2} t^{2} - 0.0416666666666667 L^{2} T^{5} a^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} b^{2} t^{3} - 0.0416666666666667 L^{2} T^{5} h^{2} t^{3} + 0.0208333333333333 L^{2} T^{4} a^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} b^{2} t^{4} + 0.0208333333333333 L^{2} T^{4} h^{2} t^{4} - 0.000651041666666667 T^{8} a^{4} + 0.00130208333333333 T^{8} a^{2} b^{2} + 0.00130208333333333 T^{8} a^{2} h^{2} - 0.000651041666666667 T^{8} b^{4} - 0.00130208333333333 T^{8} b^{2} h^{2} - 0.000651041666666667 T^{8} h^{4}}}{- 16.0 L^{2} T^{2} t^{2} + 32.0 L^{2} T t^{3} - 16.0 L^{2} t^{4} + T^{4} a^{2} + 2.0 T^{4} a b + T^{4} b^{2} + T^{4} h^{2}} \right)} \right)}\right)}\]

Zdvihová závislost a převodové funkce

Zdvihová závilost \(\phi(l)\) je přímo výraz pro \(\Psi\). Převodovou funkci \(\mu = \frac{d\phi}{dl}\) nalezneme snadno z (4):

\[ \begin{equation} b\sin(\phi)\frac{d\phi}{dl} + h\cos(\phi)\frac{d\phi}{dl} = \frac{2l(t)}{2a} \end{equation} \]

\[ \begin{equation} \frac{d\phi}{dl} = \frac{l(t)}{a\Big(b\sin(\phi) + h\cos(\phi)\Big)} \tag{6} \end{equation} \]

Vykreslení kinematických veličin

import matplotlib.pyplot as plt
import numpy as np
import warnings
warnings.filterwarnings('ignore')
plt.xkcd()
plt.figure(figsize=(15, 5))
a_num, b_num, c_num, d_num, h_num = 1., 2., 3., 0.5, 0.5
T_num, L_num = 1., 2.
tn = np.linspace(0.1, 1., 101)

pp = {a:a_num, b:b_num, c:c_num, d:d_num, h:h_num, T:T_num, L:L_num}
phin = sp.lambdify(t, phi.subs(pp))
omegan = sp.lambdify(t, omega.subs(pp))
alphan = sp.lambdify(t, alpha.subs(pp))
ln = sp.lambdify(t, l.subs(pp))

<Figure size 1080x360 with 0 Axes>

plt.plot(tn, ln(tn))
plt.title('Zdvihova funkce')

Text(0.5, 1.0, 'Zdvihova funkce')

findfont: Font family ['xkcd', 'xkcd Script', 'Humor Sans', 'Comic Neue', 'Comic Sans MS', 'StayPuft'] not found. Falling back to DejaVu Sans.

plt.plot(tn, np.rad2deg(phin(tn)))
plt.title('natoceni')

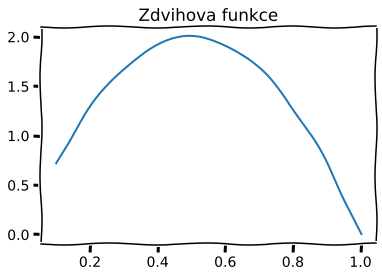
Text(0.5, 1.0, 'natoceni')

plt.plot(tn, omegan(tn))
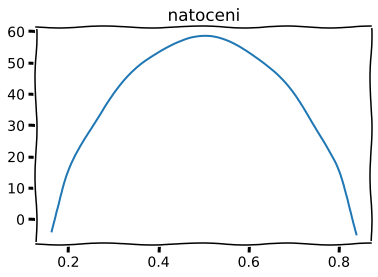
plt.title('uhlova rychlost')

Text(0.5, 1.0, 'uhlova rychlost')

plt.plot(tn, alphan(tn))
plt.title('uhlove zrychleni')

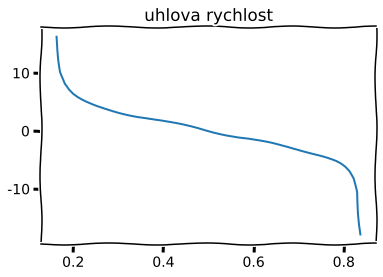
Text(0.5, 1.0, 'uhlove zrychleni')

dphidl = l / a / (b * sp.sin(phi) + h * sp.cos(phi))
dphidln = sp.lambdify(t, dphidl.subs(pp))
plt.plot(tn, dphidln(tn))
plt.title('prvni prevodova funkce')

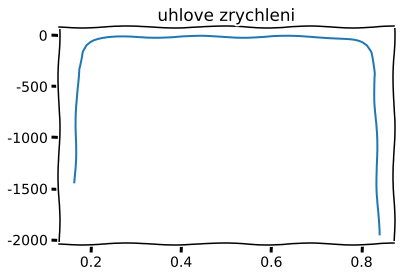
Text(0.5, 1.0, 'prvni prevodova funkce')